Catene di Markov
Esempi
Mescolamento di carte. Si considera un mazzo di n carte numerate da 1 a n. Ad ogni passo si sceglie una carta a caso e la si sposta in cima al mazzo. Lo stato X_k rappresenta la disposizione delle carte dopo k mosse. Lo spazio degli stati è l’insieme delle permutazioni di n elementi, di cardinalità n!.
In questo caso si vuole studiare quante mosse sono necessarie affinché la disposizione delle carte sia “quasi quella uniforme”.
Modello di Ehrenfest. (scambio di particelle tra due urne). Si hanno due urne con un totale di m palline. Lo stato X_n rappresenta il numero di palline nell’urna 1 al tempo n. Lo spazio degli stati è S = \{0, 1, \dots, m\}.
A ogni passo si sceglie una pallina a caso tra le m e la si sposta nell’altra urna.
P_{x,y} = \begin{cases}
\dfrac{m-x}{m} & \text{se } y = x+1 \\[0.75em]
\dfrac{x}{m} & \text{se } y = x-1 \\[0.75em]
0 & \text{altrimenti}
\end{cases}In particolare P_{m, m-1} = 1 e P_{0, 1} = 1.
Rappresentazione tramite grafo. Una catena di Markov può essere rappresentata come un grafo orientato dove i nodi sono gli stati in S e gli archi pesati rappresentano quelle che chiameremo probabilità di transizione p_{x,y} > 0.
Passeggiata aleatoria su un grafo. Sia G = (V, E) un grafo non orientato. Lo spazio degli stati è S = V. A ogni passo, se ci troviamo nel vertice x, ci spostiamo in uno dei suoi vicini scelto uniformemente. La matrice di transizione è:
P_{x,y} = \begin{cases}
\dfrac{1}{d(x)} & \text{se } \{x, y\} \in E \\[0.75em]
0 & \text{altrimenti}
\end{cases}dove d(x) è il grado del vertice x.
Passeggiata aleatoria su \mathbb{Z}^d. Siano (X_n)_{n \ge 1} variabili aleatorie indipendenti e identicamente distribuite, con distribuzione uniforme su \{\pm e_1, \dots, \pm e_d\}, dove e_j sono i vettori della base canonica di \mathbb{Z}^d. Sia S_0 il punto iniziale. La posizione al tempo n è data da:
S_n = S_0 + \sum_{k=1}^n X_kSi ha che S_{n+1} = S_n + X_{n+1}, quindi il processo è una catena di Markov con probabilità di transizione p_{x,y} = \mathbb{P}[X_1 = y-x].
Problema della rovina del giocatore: sia p la probabilità di vincita e 1-p la probabilità di perdita. Supponiamo di avere un capitale iniziale di k unità e che a ogni scommessa venga giocata 1 unità; il problema è: qual è la probabilità di bancarotta?
Filtrazione e proprietà comune
§ Sia (\Omega, \mathcal{F}, \mathbb{P}) uno spazio di probabilità allora una filtrazione è una famiglia (\mathcal{F}_n)_{n \ge 0} crescente di \sigma-algebre contenute in \mathcal{F}, cioè
\mathcal{F}_0 \subseteq \mathcal{F}_1 \subseteq \mathcal{F}_2 \subseteq \cdots \subseteq \mathcal{F}.La caratteristica comune ai processi di interesse è che descrivono il passaggio da uno stato all’altro (transizioni).
Osservazione. Useremo la notazione \mathbb{P}[A \mid \mathcal{F}] = \mathbb{E}[\bbone_A \mid \mathcal{F}] per la probabilità condizionata di un evento A data la \sigma-algebra \mathcal{F}_n.
In particolare, si può verificare che se \mathcal{F} = \sigma(\bbone_B) per un evento B allora
\mathbb{P}[A \mid \mathcal{F}]
= \mathbb{E}[\bbone_A \mid \bbone_B]
= \frac{\mathbb{P}[A \cap B]}{\mathbb{P}[B]} \bbone_B + \frac{\mathbb{P}[A \cap B^\complement]}{\mathbb{P}[B^\complement]} \bbone_{B^\complement}§ Definizione. Sia S uno spazio di stati (al più numerabile). Data una famiglia di variabili aleatorie (X_n)_{n\ge 0} a valori in S ed una filtrazione (\mathcal{F}_n)_{n\ge 0} tale che ogni X_n sia \mathcal{F}_n-misurabile, con \mathcal{F}_n = \sigma(X_0, X_1, \dots, X_n), allora (X_n)_{n\ge 0} è detta catena di Markov se per ogni n\ge 0 e per ogni x\in S vale
\mathbb{P}[X_{n+1}=x \mid \mathcal{F}_n] = \mathbb{P}[X_{n+1}=x \mid X_n].In particolare, prendendo la filtrazione naturale \mathcal{F}_n = \sigma(X_0,\dots,X_n) la proprietà si può scrivere come
\mathbb{P}[X_{n+1}=x \mid X_0,\dots,X_n] = \mathbb{P}[X_{n+1}=x \mid X_n].Verifichiamo che questo definizione cattura l’intuizione di “memoria limitata” ovvero la cosiddetta proprietà di Markov:
\mathbb{P}[X_{n+1}=x \mid X_0,\dots,X_n] = \mathbb{P}[X_{n+1}=x \mid X_n]§ Proposizione. Una famiglia di variabili aleatorie (X_n)_{n\ge 0} a valori in S è una catena di Markov se e solo se per ogni n\ge 1 e per ogni y,x_0,x_1,\dots,x_n\in S tali che
\mathbb{P}[X_0=x_0,\dots,X_n=x_n]>0 vale
\mathbb{P}[X_{n+1}=y \mid X_0=x_0,\dots,X_n=x_n]
=
\mathbb{P}[X_{n+1}=y \mid X_n=x_n].Dimostrazione. Sia \mathcal{F}_n=\sigma(X_0,\dots,X_n) è generata dagli eventi \{X_0=x_0,\dots,X_n=x_n\}_{x_0,\dots,x_n\in S}. Fissato A=\{X_0=x_0,\dots,X_n=x_n\}, dalla definizione di condizionale rispetto a \mathcal{F}_n si ha
\begin{aligned}
\mathbb{E}\left[\mathbb{P}[X_{n+1}=x \mid \mathcal{F}_n]\bbone_A\right]
&= \mathbb{E}\left[\mathbb{E}[\bbone_{\{X_{n+1}=x\}} \mid \mathcal{F}_n]\bbone_A\right] \\
&= \mathbb{E}\left[\bbone_{\{X_{n+1}=x\}}\bbone_A\right] \\
&= \mathbb{P}[\{X_{n+1}=x\}\cap A] \\
&= \mathbb{P}[X_{n+1}=x \mid X_0=x_0,\dots,X_n=x_n]\,\mathbb{P}[A]
\end{aligned}Ora osseriamo che
\mathbb{P}[X_{n+1}=x \mid X_n]=\sum_{z\in S}\mathbb{P}[X_{n+1}=x \mid X_n=z]\bbone_{\{X_n=z\}}\begin{aligned}
\mathbb{E}\left[\mathbb{P}[X_{n+1}=x \mid X_n]\bbone_A\right]
&= \sum_{z\in S}\mathbb{P}[X_{n+1}=x \mid X_n=z]\,\mathbb{P}[A\cap\{X_n=z\}] \\
&= \mathbb{P}[X_{n+1}=x \mid X_n=x_n]\,\mathbb{P}[A]
\end{aligned}Confrontando le due uguaglianze si ottiene \mathbb{P}[X_{n+1}=x \mid X_0=x_0,\dots,X_n=x_n]=\mathbb{P}[X_{n+1}=x \mid X_n=x_n], che è la tesi. \square
Matrice di transizione e distribuzione iniziale
§ Una catena di Markov (X_n)_{n \ge 0} si dice omogenea se la probabilità di transizione non dipende dal tempo n, ovvero:
\mathbb{P}[X_{n+1} = y \mid X_n = x] = p_{x,y}per ogni n \ge 0 e ogni x, y \in S.
Osservazione. Sia (X_n)_{n \in \mathbb{N}} una catena di Markov omogenea. Definiamo:
-
q_x = \mathbb{P}[X_0 = x]perx \in S(distribuzione iniziale) -
p_{x,y} = \mathbb{P}[X_{n+1} = y \mid X_n = x]perx, y \in S(matrice di transizione)
Si ha che:
\mathbb{P}[X_{n+1} = y \mid X_n] = \sum_{x \in S} \mathbb{P}[X_{n+1} = y \mid X_n = x] \bbone_{\{X_n = x\}} = \left( \sum_{x \in S} p_{x,y} \bbone_{\{x\}} \right)(X_n)§ Teorema. (X_n)_{n \in \mathbb{N}} è una catena di Markov omogenea se e solo se vale:
\mathbb{P}[X_0 = x_0, \dots, X_n = x_n] = q_{x_0} \, p_{x_0, x_1} \, p_{x_1, x_2} \cdots p_{x_{n-1}, x_n}per ogni n \ge 0 e ogni x_0, x_1, \dots, x_n \in S.
Dimostrazione.
(\Rightarrow) Supponiamo che (X_n) sia una catena di Markov. Procediamo per induzione su n.
-
Caso base (
n=0):\mathbb{P}[X_0 = x_0] = q_{x_0}per definizione. -
Caso induttivo: Supponiamo vero per
n-1. Allora:
\begin{aligned}
\mathbb{P}[X_0 = x_0, \dots, X_n = x_n]
&= \mathbb{P}[X_0 = x_0, \dots, X_{n-1} = x_{n-1}] \cdot \mathbb{P}[X_n = x_n \mid X_0 = x_0, \dots, X_{n-1} = x_{n-1}] \\
&= q_{x_0} \, p_{x_0, x_1} \cdots p_{x_{n-2}, x_{n-1}} \cdot \mathbb{P}[X_n = x_n \mid X_n = x_{n-1}] \\
&= q_{x_0} \, p_{x_0, x_1} \cdots p_{x_{n-2}, x_{n-1}} \cdot p_{x_{n-1}, x_n}
\end{aligned}dove abbiamo usato la proprietà di Markov nel secondo passaggio e la definizione di p_{x,y} nel terzo passaggio.
(\Leftarrow) Supponiamo che valga la fattorizzazione. Allora:
\mathbb{P}[X_{n+1} = y \mid X_0 = x_0, \dots, X_n = x_n] = \frac{\mathbb{P}[X_0 = x_0, \dots, X_n = x_n, X_{n+1} = y]}{\mathbb{P}[X_0 = x_0, \dots, X_n = x_n]}= \frac{q_{x_0} \, p_{x_0, x_1} \cdots p_{x_{n-1}, x_n} \, p_{x_n, y}}{q_{x_0} \, p_{x_0, x_1} \cdots p_{x_{n-1}, x_n}} = p_{x_n, y} = \mathbb{P}[X_{n+1} = y \mid X_n = x_n]che è la proprietà di Markov. \square
Osservazione. (p_{x,y})_{x,y \in S} è una matrice stocastica, ovvero:
\sum_{y \in S} p_{x,y} = 1 \quad \text{per ogni } x \in Se \sum_x q_x = 1 è la distribuzione iniziale.
§ Proposizione. Sia Q = (q_x)_{x \in S} e P = (p_{x,y})_{x,y \in S}. Allora:
- La legge di
X_nèQ P^n. - La legge condizionale di
X_{n+m}datoX_nèP^m, ovvero:\mathbb{P}[X_{n+m} = y \mid X_n = x] = (P^m)_{x,y}
Ricordiamo (principalmente per ricordare gli indici giusti) che date A = (a_{i,j})_{i,j=1}^{m,n} e B = (b_{i,j})_{i,j=1}^{n,p} per il prodotto matriciale vale:
(AB)_{i,j} = \sum_{k=1}^n a_{i,k} b_{k,j}dove il risultato è una matrice di taglia m \times p.
Osservazione (Equazioni di Chapman-Kolmogorov). Vale la relazione P^{n+m} = P^n P^m, ovvero:
\mathbb{P}[X_{n+m} = y \mid X_0 = x] = (P^{n+m})_{x,y} = \sum_{z \in S} (P^n)_{x,z} (P^m)_{z,y}Dimostrazione. Per induzione su n \ge 0:
-
Caso base (
n=0):\mathbb{P}[X_0 = y] = q_y = (Q P^0)_y, vera ovviamente. -
Passo induttivo: Supponiamo che la legge di
X_nsiaQ P^n. Allora:\begin{aligned} \mathbb{P}[X_{n+1} = y] &= \sum_{x \in S} \mathbb{P}[X_{n+1} = y \mid X_n = x] \mathbb{P}[X_n = x] \\ &= \sum_{x \in S} p_{x,y} \mathbb{P}[X_n = x] \\ &= \sum_{x \in S} (Q P^n)_x p_{x,y} \\ &= ((Q P^n) \cdot P)_y = (Q P^{n+1})_y \end{aligned}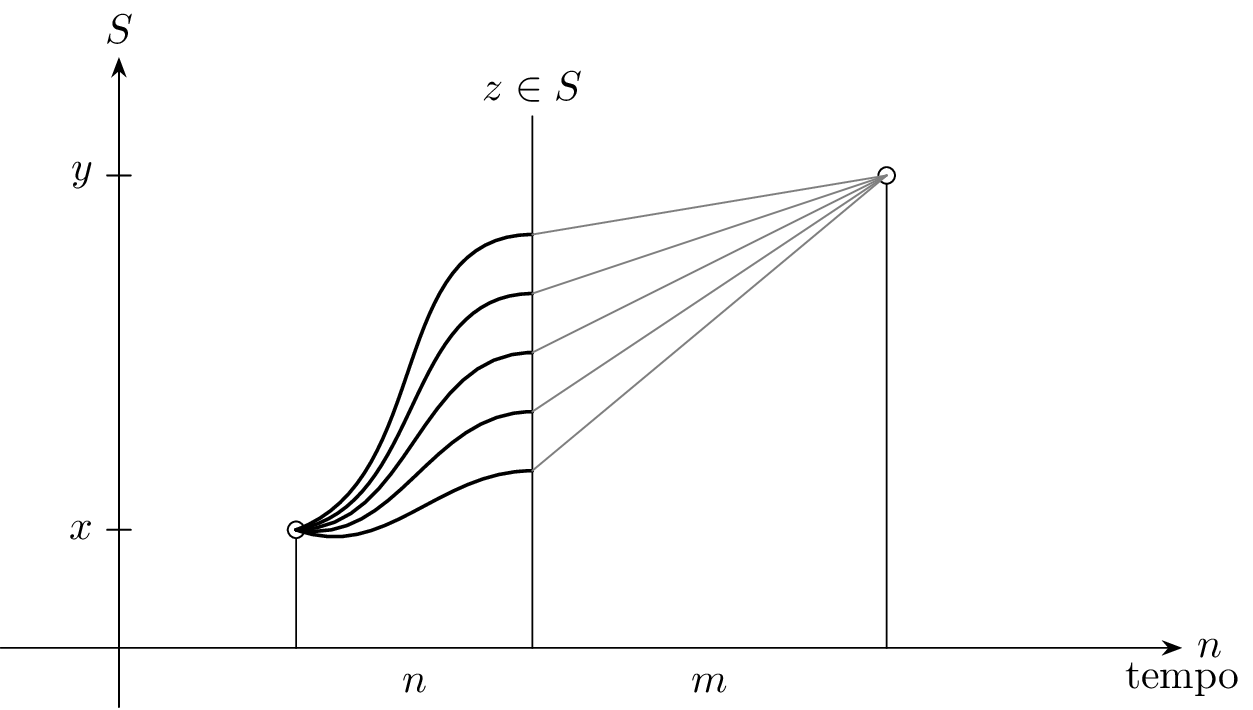
E analogamente per la seconda affermazione.
\square
§ Teorema. Sia (X_n)_{n \in \mathbb{N}} una catena di Markov. Allora per ogni n \ge 0, la catena passata (X_{n+m})_{m \le 0} è una catena di Markov indipendente da \sigma(X_0, \dots, X_{n-1}).
Dimostrazione (cenno). TODO
Tempi di arrivo
Sia (X_n)_{n \ge 0} una catena di Markov omogenea su S. Sia A \subseteq S un sottoinsieme di stati.
§ Definizione. Dato A \subseteq S, allora la variabile aleatoria U_A, detta tempo di primo arrivo in A, è definita come:
U_A = \inf \{n \ge 0 : X_n \in A\}con la convenzione \inf(\varnothing) = +\infty. Definiamo inoltre:
-
a_{A,x} = \mathbb{P}[U_A < \infty \mid X_0 = x], la probabilità di passare daApartendo dax. (forse detta hitting probability??) -
m_{A,x} = \mathbb{E}[U_A \mid X_0 = x], il tempo medio di arrivo inApartendo dax. (forse detta hitting time??)
§ Teorema. La famiglia (a_{A,x})_{x \in S} è la minima soluzione positiva del sistema:
\begin{cases}
a_x = 1 & \text{se } x \in A \\
a_x = \displaystyle\sum_{y \in S} p_{x,y} a_y & \text{se } x \notin A
\end{cases}Cioè, se (a_x)_{x \in S} è una soluzione tale che a_x \ge 0 per ogni x, allora a_x \ge a_{A,x} per ogni x \in S.
Dimostrazione. TODO
-
Se
x \in A, alloraU_A = 0perchéX_0 = x \in A, quindia_{A,x} = 1. Ovvero che sex \in Aallora il tempo di primo arrivo è zero quindi la probabilità di arrivare inAè banalmente1. -
Se invece
x \notin A, allora:\begin{aligned} a_{A,x} &= \mathbb{P}[U_A < \infty \mid X_0 = x] \\ &= \sum_{y \in S} \mathbb{P}[U_A < \infty, X_1 = y \mid X_0 = x] \\ &= \sum_{y \in S} \mathbb{P}[U_A < \infty \mid X_0 = x, X_1 = y] \mathbb{P}[X_1 = y \mid X_0 = x] \\ &= \sum_{y \in S} \mathbb{P}[U_A < \infty \mid X_0 = x, X_1 = y] p_{x,y} \end{aligned}Ora osserviamo che
\mathbb{P}[U_A < \infty \mid X_0 = x, X_1 = y] = a_{A,y}:\begin{aligned} \mathbb{P}[U_A < \infty \mid X_0 = x, X_1 = y] &= \mathbb{P}[\exists n \ge 0 \text{ t.c. } X_n \in A \mid X_0 = x, X_1 = y] \\ &= \mathbb{P}[\exists n \ge 1 \text{ t.c. } X_n \in A \mid X_0 = x, X_1 = y] \\ &= \mathbb{P}[\exists n \ge 0 \text{ t.c. } X_{n+1} \in A \mid X_1 = y] \end{aligned}Sia
(Y_n)_{n \ge 0} = (X_{n+1})_{n \ge 0}. Allora:\mathbb{P}[\exists n \ge 0 \text{ t.c. } Y_n \in A \mid Y_0 = y] = \mathbb{P}[\exists n \ge 0 \text{ t.c. } X_n \in A \mid X_0 = y] = a_{A,y}perché
(Y_n)_{n \ge 0}ha la stessa legge di(X_n)_{n \ge 0}seX_0 = Y_0 = y.
Sia ora (a_x)_{x \in S} una soluzione positiva del sistema.
-
Se
x \in A, alloraa_x = 1 = a_{A,x}. -
Se
x \notin A, allora:\begin{aligned} a_x &= \sum_{y \in S} p_{x,y} a_y = \sum_{y \in A} p_{x,y} + \sum_{y \notin A} p_{x,y} a_y \\ &= \mathbb{P}[X_1 \in A \mid X_0 = x] + \sum_{y \notin A} p_{x,y} a_y \\ &= \mathbb{P}[U_A = 1 \mid X_0 = x] + \sum_{y_1 \notin A} p_{x,y_1} \left( \sum_{y_2 \in S} p_{y_1,y_2} a_{y_2} \right) \\ &= \mathbb{P}[U_A = 1 \mid X_0 = x] + \sum_{y_1 \notin A} \sum_{y_2 \in A} p_{x,y_1} p_{y_1,y_2} + \sum_{y_1 \notin A} \sum_{y_2 \notin A} p_{x,y_1} p_{y_1,y_2} a_{y_2} \\ &= \mathbb{P}[U_A = 1 \mid X_0 = x] + \mathbb{P}[U_A = 2 \mid X_0 = x] + \sum_{y_1 \notin A} \sum_{y_2 \notin A} p_{x,y_1} p_{y_1,y_2} a_{y_2} \\ &= \mathbb{P}[U_A \le 2 \mid X_0 = x] + \sum_{y_1 \notin A} \sum_{y_2 \notin A} p_{x,y_1} p_{y_1,y_2} a_{y_2} \end{aligned}Iterando, per ogni
m \in \mathbb{N}si ha:a_x = \mathbb{P}[U_A \le m \mid X_0 = x] + \sum_{y_1, \dots, y_m \notin A} p_{x,y_1} p_{y_1,y_2} \cdots p_{y_{m-1},y_m} a_{y_m}Poiché
a_y \ge 0, il termine della sommatoria è non negativo, quindi:a_x \ge \mathbb{P}[U_A \le m \mid X_0 = x]Mandando
m \to \infty, per la continuità della probabilità si ottiene:a_x \ge \mathbb{P}[U_A < \infty \mid X_0 = x] = a_{A,x}che prova la minimalità.
\square
§ Corollario. La famiglia (m_{A,x})_{x \in S} è la minima soluzione positiva del sistema:
\begin{cases}
m_x = 0 & \text{se } x \in A \\
m_x = 1 + \displaystyle\sum_{y \notin A} p_{x,y} m_y & \text{se } x \notin A
\end{cases}Rovina della giocatrice
Esempio. TODO
Consideriamo una passeggiata aleatoria su \mathbb{N} con probabilità di vittoria p \in (0, 1) e probabilità di perdita 1-p. Sia A = \{0\} lo stato assorbente (la rovina). Vogliamo calcolare a_k = \mathbb{P}[U_A < \infty \mid X_0 = k], ovvero la probabilità di rovina partendo da un capitale k.
Sappiamo che a_0 = 1 e per k > 0 vale la relazione di ricorrenza:
a_k = p a_{k+1} + (1-p) a_{k-1}che possiamo riscrivere come:
a_k - a_{k+1} = \underbrace{\frac{1-p}{p}}_{=\lambda} (a_{k-1} - a_k) \implies a_k - a_{k+1} = \lambda^k (a_0 - a_1)Analizziamo i diversi casi per \lambda:
-
Se
\lambda > 1(ovverop < 1/2): Poiché\lambda^k \to +\inftyperk \to \infty, e sapendo che0 \le a_k \le 1, l’unica possibilità è chea_0 - a_1 = 0, ovveroa_1 = a_0 = 1. Di conseguenza:a_k = 1 \quad \forall k \ge 0. -
Se
\lambda = 1(ovverop = 1/2): Abbiamoa_k - a_{k+1} = a_0 - a_1. Sommando perjda0ak-1:a_0 - a_k = \sum_{j=0}^{k-1} (a_j - a_{j+1}) = k(a_0 - a_1)Poiché
a_kdeve rimanere limitato tra0e1per ognik, deve esserea_0 - a_1 = 0, quindia_1 = a_0 = 1e:a_k = 1 \quad \forall k \ge 0. -
Se
\lambda < 1(ovverop > 1/2): Sommando la progressione geometrica:\begin{aligned} a_0 - a_k &= \sum_{j=0}^{k-1} (a_j - a_{j+1}) \\ &= (a_0 - a_1) \sum_{j=0}^{k-1} \lambda^j \\ &= \frac{(a_0 - a_1)(1-\lambda^k)}{1-\lambda} \end{aligned}Poiché
\lim_{k \to \infty} a_k \ge 0, allora la successione(a_k)_{k \ge 0}è positiva, cioè:1 - \frac{1-a_1}{1-\lambda} \ge 0 \implies a_1 \ge \lambdaEssendo
a_kla minima soluzione positiva, scegliamoa_1 = \lambda, da cui:a_{\{0\}, k} = \lambda^k = \left( \frac{1-p}{p} \right)^k.
Passeggiata aleatoria su \mathbb{Z}
Anche a tutto schermo qui: Passeggiata aleatoria su $\mathbb{Z}$.
Stati ricorrenti e transienti
§ Sia (X_n)_{n \ge 0} una catena di Markov a valori in S. Per ogni x \in S definiamo:
U_x \coloneqq \inf \{n \ge 0 : X_n = x\}, il tempo di primo arrivo inx.T_x \coloneqq \inf \{n \ge 1 : X_n = x\}, il tempo di primo passaggio (o ritorno) inx.
Definiamo inoltre:
p_{x,y}(n) \coloneqq \mathbb{P}[X_n = y \mid X_0 = x], conp_{x,y}(0) = \delta_{x,y}.f_{x,y}(n) \coloneqq \mathbb{P}[T_y = n \mid X_0 = x], conf_{x,y}(0) = 0.f_{x,y} \coloneqq \sum_{n=1}^\infty f_{x,y}(n) = \mathbb{P}[T_y < \infty \mid X_0 = x].
Si osservi che x è ricorrente se e solo se f_{x,x} = 1.
§ Definizione. Sia (X_n)_{n \ge 0} una catena di Markov a valori in S. Indichiamo il numero di visite allo stato x \in S come
N_x \coloneqq \sum_{n=0}^\infty \bbone_{\{X_n = x\}}.Allora diciamo che un elemento x \in S è ricorrente (o rispettivamente transiente) se:
\mathbb{P}[\exists n \ge 1 : X_n = x \mid X_0 = x] = 1
\quad (\text{risp. } < 1).§ Teorema (di Abel). Sia G(t) = \sum_{n=0}^\infty a_n t^n una serie di potenze convergente per |t| < 1. Allora:
- Se
\sum a_nconverge, alloraG(t) \xrightarrow{t \uparrow 1} \sum a_n. - Se
\sum a_n = \infty, alloraG(t) \xrightarrow{t \uparrow 1} \infty.
§ Lemma. Siano P_{x,y}(t) = \sum_{n=0}^\infty p_{x,y}(n) t^n e F_{x,y}(t) = \sum_{n=0}^\infty f_{x,y}(n) t^n. Allora per ogni t \in (-1, 1) vale:
P_{x,y}(t) = \delta_{x,y} + F_{x,y}(t) P_{y,y}(t)Dimostrazione. Per ogni m \ge 1, siano gli eventi A_m = \{X_m = y\} e B_j = \{X_1 \neq y, \dots, X_{j-1} \neq y, X_j = y\} (primo passaggio in y al tempo j). Allora:
p_{x,y}(m) = \mathbb{P}[A_m \mid X_0 = x] = \sum_{j=1}^m \mathbb{P}[A_m \cap B_j \mid X_0 = x]Usando la proprietà di Markov:
\begin{aligned}
\mathbb{P}[A_m \cap B_j \mid X_0 = x] &= \mathbb{P}[X_m = y \mid X_j = y, B_j, X_0 = x] \mathbb{P}[B_j \mid X_0 = x] \\
&= \mathbb{P}[X_m = y \mid X_j = y] f_{x,y}(j) \\
&= p_{y,y}(m-j) f_{x,y}(j)
\end{aligned}Quindi p_{x,y}(m) = \sum_{j=1}^m f_{x,y}(j) p_{y,y}(m-j). Moltiplicando per t^m e sommando su m \ge 1:
\begin{aligned}
\sum_{m=1}^\infty p_{x,y}(m) t^m &= \sum_{m=1}^\infty \left( \sum_{j=1}^m f_{x,y}(j) t^j p_{y,y}(m-j) t^{m-j} \right) \\
&= \left( \sum_{j=1}^\infty f_{x,y}(j) t^j \right) \left( \sum_{k=0}^\infty p_{y,y}(k) t^k \right) \\
&= F_{x,y}(t) P_{y,y}(t)
\end{aligned}Aggiungendo il termine m=0 (che è p_{x,y}(0) = \delta_{x,y}), otteniamo la tesi. \square
§ Proposizione. Siano x, y \in S. Allora:
yè ricorrente\iff \mathbb{E}[N_y \mid X_0 = y] = \infty. In tal caso, sef_{x,y} > 0, allora\mathbb{E}[N_y \mid X_0 = x] = \infty.yè transiente\iff \mathbb{E}[N_y \mid X_0 = y] < \infty. In tal caso, sef_{x,y} > 0, allora\mathbb{E}[N_y \mid X_0 = x] < \infty.
In particolare vale la relazione:
\mathbb{E}[N_y \mid X_0 = x] = \sum_{n=0}^\infty p_{x,y}(n).Dimostrazione. Dimostriamo il punto 1 (il punto 2 è analogo).
Supponiamo x = y. Dalla relazione del lemma abbiamo P_{x,x}(t) = 1 + F_{x,x}(t) P_{x,x}(t), da cui:
P_{x,x}(t) = \frac{1}{1 - F_{x,x}(t)}Ricordiamo che x è ricorrente se e solo se f_{x,x} = 1.
- Se per assurdo
\sum_{n=0}^\infty p_{x,x}(n) < \infty, allora per il teorema di AbelP_{x,x}(t) \xrightarrow{t \uparrow 1} \sum p_{x,x}(n) < \infty. Tuttavia, sexè ricorrente,F_{x,x}(t) \xrightarrow{t \uparrow 1} f_{x,x} = 1, quindiP_{x,x}(t) \to \infty, assurdo. - Viceversa, se
\sum_{n=0}^\infty p_{x,x}(n) = \infty, alloraP_{x,x}(t) \xrightarrow{t \uparrow 1} \infty. Dalla relazioneP_{x,x}(t) = \frac{1}{1 - F_{x,x}(t)}, questo implicaF_{x,x}(t) \xrightarrow{t \uparrow 1} 1, ovverof_{x,x} = 1, quindixè ricorrente.\square
§ Proposizione. Sia x \in S. Allora:
xè ricorrente\iff \mathbb{P}[N_x = \infty \mid X_0 = x] = 1.xè transiente\iff \mathbb{P}[N_x = \infty \mid X_0 = x] = 0.
Dimostrazione. Facciamo vedere che \mathbb{P}[N_x > K \mid X_0 = x] = f_{x,x}^K. Procediamo per induzione su K:
-
Caso base (
K=0): Vero, perché\mathbb{P}[N_x > 0 \mid X_0 = x] = 1 = f_{x,x}^0. -
Passo induttivo: Sia
K > 0. DefiniamoB_n = \{X_1 \neq x, \dots, X_{n-1} \neq x, X_n = x\}l’evento del primo ritorno inxal tempon. Allora:\begin{aligned} \mathbb{P}[N_x > K \mid X_0 = x] &= \sum_{n=1}^\infty \mathbb{P}[N_x > K, B_n \mid X_0 = x] \\ &= \sum_{n=1}^\infty \mathbb{P}[N_x > K \mid X_0 = x, B_n] f_{x,x}(n) \end{aligned}Condizionatamente a
B_n(e quindi aX_n = x), il numero di visite totaliN_xè dato dalla visita al temponpiù le visite successive. SiaN_x^{(n)}il numero di visite della catena traslata(X_{m+n})_{m \ge 0}. AlloraN_x = 1 + N_x^{(n)}. Per la proprietà di Markov:\begin{aligned} \mathbb{P}[N_x > K \mid X_0 = x, B_n] &= \mathbb{P}[1 + N_x^{(n)} > K \mid X_n = x] \\ &= \mathbb{P}[N_x^{(n)} > K-1 \mid X_n = x] \end{aligned}Per l’omogeneità della catena, quest’ultima probabilità è uguale a
\mathbb{P}[N_x > K-1 \mid X_0 = x], che per ipotesi induttiva èf_{x,x}^{K-1}. Dunque:\begin{aligned} \mathbb{P}[N_x > K \mid X_0 = x] &= \sum_{n=1}^\infty f_{x,x}^{K-1} f_{x,x}(n) \\ &= f_{x,x}^{K-1} \sum_{n=1}^\infty f_{x,x}(n) \\ &= f_{x,x}^{K-1} f_{x,x} \\ &= f_{x,x}^K \end{aligned}
Concludendo:
- Se
xè ricorrente,f_{x,x} = 1, quindi\mathbb{P}[N_x > K \mid X_0 = x] = 1per ogniK, da cui\mathbb{P}[N_x = \infty \mid X_0 = x] = 1. - Se
xè transiente,f_{x,x} < 1, quindi\mathbb{P}[N_x > K \mid X_0 = x] = f_{x,x}^K \xrightarrow{K \to \infty} 0, da cui\mathbb{P}[N_x = \infty \mid X_0 = x] = 0. In questo caso vale anche\mathbb{P}[N_x \le K \mid X_0 = x] = 1 - f_{x,x}^K.\square
Comunicazione tra stati
§ Definizione. Sia (X_n)_{n \ge 0} una catena di Markov a valori in S. Allora dati x, y \in S, si dice che x conduce a y se
\mathbb{P}[\exists n \ge 0 : X_n = y \mid X_0 = x] > 0e si indica con x \to y. Si dice che x e y comunicano se x \to y e y \to x, e si indica con x \leftrightarrow y.
§ Proposizione. Dati x, y \in S, Sono equivalenti:
-
x \to y. -
Esistono
n \ge 0e una successione di statiz_0, z_1, \dots, z_ntali chez_0 = x,z_n = yep_{z_i, z_{i+1}} > 0per ognii \in \{0, \dots, n-1\}. -
Esiste
n \ge 0tale chep_{x,y}(n) > 0. -
f_{x,y} > 0.
Dimostrazione.
-
i.
\Leftrightarrowii.)L’evento\{\exists n \ge 0 : X_n = y\}è l’unione\bigcup_{n=0}^\infty \{X_n = y\}. Per un fissatonvale:\begin{aligned} p_{x,y}(n) &= \mathbb{P}[X_n = y \mid X_0 = x] \\[0.5em] &\le \mathbb{P}[\exists m \ge 0 : X_m = y \mid X_0 = x] \\ &\le \sum_{m=0}^\infty \mathbb{P}[X_m = y \mid X_0 = x] \end{aligned}Se
\mathbb{P}[\exists m \ge 0 : X_m = y \mid X_0 = x] > 0, allora deve esistere almeno unm \ge 0tale chep_{x,y}(m) > 0. Viceversa, sep_{x,y}(n) > 0per qualchen, allora la probabilità dell’unione è strettamente positiva. -
ii.
\Leftrightarrowiii.)Ricordando chep_{x,y}(n) = \sum_{z_1, \dots, z_{n-1} \in S} p_{x, z_1} p_{z_1, z_2} \dots p_{z_{n-1}, y}, si ha chep_{x,y}(n) > 0se e solo se esiste almeno un camminox, z_1, \dots, z_{n-1}, ycon probabilità di transizione positive. -
iv.
\Leftrightarrowiii.)Siaf_{x,y} = \sum_{n=1}^\infty f_{x,y}(n), dovef_{x,y}(n) = \mathbb{P}[X_1 \neq y, \dots, X_{n-1} \neq y, X_n = y \mid X_0 = x]. Poichéf_{x,y}(n) \le p_{x,y}(n), sef_{x,y} > 0allora esisten \ge 1tale chef_{x,y}(n) > 0, e quindip_{x,y}(n) > 0. Viceversa, supponiamop_{x, z_1} \dots p_{z_{n-1}, y} > 0. Siam = \min \{k \ge 1 \mid z_k = y\}. Allora il camminox, z_1, \dots, z_{m-1}, ynon visitayprima del tempom, dunquef_{x,y}(m) \ge p_{x, z_1} \dots p_{z_{m-1}, y} > 0, il che implicaf_{x,y} > 0.\square
§ Definizione. Sia (X_n)_{n \ge 0} una catena di Markov a valori in S e sia C \subseteq S.
Csi dice chiuso se per ognix \in C,x \to y \implies y \in C.Csi dice irriducibile sex \leftrightarrow yper ognix, y \in C.
Osservazione. Uno stato x \in S si dice assorbente se \{x\} è un insieme chiuso.
Osservazione. C è chiuso se e solo se per ogni x \in C e y \in S, p_{x,y} > 0 \implies y \in C.
Osservazione. La comunicazione "\leftrightarrow" è una relazione di equivalenza su S.
Dimostrazione.
La riflessività (x \leftrightarrow x) e la simmetria (x \leftrightarrow y \implies y \leftrightarrow x) seguono banalmente dalla definizione.
Verifichiamo la transitività: x \to y e y \to z \implies x \to z.
Se x \to y e y \to z, allora esistono m, k \ge 0 tali che p_{x,y}(m) > 0 e p_{y,z}(k) > 0. Per le equazioni di Chapman-Kolmogorov:
p_{x,z}(m+k) = \sum_{u \in S} p_{x,u}(m) p_{u,z}(k) \ge p_{x,y}(m) p_{y,z}(k) > 0Quindi x \to z. \square
§ Proposizione. Sia (X_n)_{n \ge 0} una catena di Markov su S e sia C \subseteq S.
- Se
Cè chiuso e finito, allora ognix \in Cè ricorrente. - Se
Cè una classe di equivalenza di stati ricorrenti, alloraCè chiuso. - Se
Cè una classe di equivalenza, allora gli stati diCsono o tutti ricorrenti o tutti transienti.
Dimostrazione. TODO
-
Sia
Cchiuso e finito e siax \in C. Se per assurdoxfosse transiente, allora per ogniy \in Csi avrebbe\sum_{n=0}^\infty p_{y,x}(n) < \infty, il che implicap_{y,x}(n) \to 0pern \to \infty. Ma poichéCè chiuso,\sum_{y \in C} p_{x,y}(n) = 1per ognin. Se tutti gli stati fossero transienti, avremmo:1 = \sum_{y \in C} p_{x,y}(n) \xrightarrow{n \to \infty} 0che è assurdo.
-
Sia
Cuna classe di equivalenza di stati tutti ricorrenti. Se per assurdoCnon fosse chiusa, esisterebberox \in Cey \notin Ctali chep_{x,y}(m) > 0per un certom(ovverox \to y). Poichéy \notin C, deve esserey \not\to x, altrimentiy \in C. Sappiamo che\mathbb{P}[\text{infiniti } n : X_n = x \mid X_0 = x] = 1. Tuttavia:\begin{aligned} \mathbb{P}[\text{infiniti } n : X_n = x \mid X_0 = x] &\le \mathbb{P}[\{N_x = \infty\} \cap \{X_m = y\}^\complement \mid X_0 = x] + \mathbb{P}[\{N_x = \infty\} \cap \{X_m = y\} \mid X_0 = x] \\ &\le \mathbb{P}[X_m \neq y \mid X_0 = x] + \mathbb{P}[N_x = \infty \mid X_m = y] p_{x,y}(m) \\ &= 1 - p_{x,y}(m) + \mathbb{P}[N_x = \infty \mid X_0 = y] p_{x,y}(m) \end{aligned}Poiché
y \not\to x, la probabilità di visitarexpartendo dayè nulla, quindi\mathbb{P}[N_x = \infty \mid X_0 = y] = 0. Allora:\mathbb{P}[\text{infiniti } n : X_n = x \mid X_0 = x] \le 1 - p_{x,y}(m) < 1che è assurdo.
-
Siano
x, y \in Stali chex \leftrightarrow y. Allora esistonok, m \ge 0tali chep_{x,y}(k) > 0ep_{y,x}(m) > 0. Per ognin \ge 0, dalle equazioni di Chapman-Kolmogorov si ha:p_{x,x}(k+n+m) \ge p_{x,y}(k) p_{y,y}(n) p_{y,x}(m)Sommando su
n \ge 0:\sum_{n=0}^\infty p_{x,x}(k+n+m) \ge p_{x,y}(k) p_{y,x}(m) \sum_{n=0}^\infty p_{y,y}(n)Se
xè transiente, allora la serie a sinistra converge, il che implica che anche la serie a destra converge (essendop_{x,y}(k) p_{y,x}(m) > 0), dunqueyè transiente. Per simmetria, seyfosse transiente anchexlo sarebbe. Quindixè ricorrente se e solo seyè ricorrente.\square
§ Teorema (di decomposizione).
Sia (X_n)_{n \ge 0} una catena di Markov omogenea su S. Allora lo spazio degli stati S può essere partizionato come:
S = T \cup \bigcup_{k \in I} C_kdove T è l’insieme di tutti gli stati transienti e ogni C_k è una classe di equivalenza chiusa, irriducibile e fatta di stati ricorrenti.
§ Lemma. Se la catena è irriducibile e ricorrente, allora \mathbb{P}[T_y < +\infty \mid X_0 = x] = 1 per ogni x, y \in S. In particolare \mathbb{P}[T_y < \infty] = 1 per ogni y.
Esempio. Se S è finito, allora esiste almeno uno stato ricorrente.
Passeggiata aleatoria su \mathbb{Z}. Consideriamo S = \mathbb{Z} con \xi_k indipendenti tali che \mathbb{P}[\xi_k = 1] = p e \mathbb{P}[\xi_k = -1] = 1-p. Sia X_n = X_0 + \sum_{k=1}^n \xi_k.
C’è una sola classe di equivalenza, dunque lo stato 0 è ricorrente (risp. transiente) se e solo se lo sono tutti gli stati.
Si ha che p_{0,0}(n) = 0 se n è dispari, mentre per passi pari:
p_{0,0}(2n) = \binom{2n}{n} p^n (1-p)^n \approx \frac{2^{2n}}{\sqrt{\pi n}} p^n (1-p)^n = \frac{1}{\sqrt{\pi n}} (4p(1-p))^ndove abbiamo usato l’approssimazione di Stirling. Analizziamo i casi per p:
- Se
p = 1/2, allora4p(1-p) = 1e\sum_n p_{0,0}(2n) \approx \sum_n \frac{1}{\sqrt{\pi n}} = \infty, quindi la catena è ricorrente. - Se
p \neq 1/2, allora4p(1-p) < 1e la serie\sum_n p_{0,0}(2n)converge, quindi la catena è transiente.
Misure Invarianti
Consideriamo ora una catena di Markov omogenea (X_n)_{n \ge 0} su S con matrice di transizione P. Una misura \mu su S è caratterizzata dalla sua densità discreta \mu = (\mu_x)_{x \in S}.
§ Definizione. Si dice che \mu è una misura invariante (o stazionaria) se \mu = \mu P, ovvero se per ogni x \in S:
\mu_x = \sum_{y \in S} \mu_y p_{y,x}.Se \mu è una probabilità, allora si dice che \mu è una legge invariante.
Osservazione. Se S è finito e se \mathbb{P}[X_n = y \mid X_0 = x] \to \pi_y per ogni x, y \in S, allora (\pi_y)_{y \in S} è una legge invariante.
Infatti, dalle equazioni di Chapman-Kolmogorov:
p_{x,y}(n+1) = \sum_{z \in S} p_{x,z}(n) p_{z,y}Mandando n \to \infty e scambiando limite e sommatoria (valido poiché S è finito):
\pi_y = \sum_{z \in S} \pi_z p_{z,y} \implies \pi = \pi P.Inoltre 1 = \sum_{y \in S} p_{x,y}(n) \to \sum_{y \in S} \pi_y, quindi \pi è effettivamente una probabilità.
Osservazione. Se X_0 ha legge invariante \pi, allora X_k ha legge \pi per ogni k \ge 1.
Infatti la legge di X_n è \pi P^n = (\pi P) P^{n-1} = \pi P^{n-1} = \dots = \pi.
Osservazione.
- Se
\muè una misura invariante, allora anche\lambda \mu = (\lambda \mu_x)_{x \in S}è una misura invariante per ogni\lambda \ge 0. - Se
\muè una misura invariante tale che0 < \sum_{x \in S} \mu_x < \infty, allora
è una legge invariante.\pi = \frac{\mu}{\sum_{x \in S} \mu_x}
Esempio (Passeggiata semplice su \mathbb{Z}).
- Se
p = 1/2, allora la misura costante\mu_k = 1per ognik \in \mathbb{Z}è una misura invariante. - Se
p \neq 1/2, le misure invarianti sono della forma\mu_k = c_1 + c_2 \left( \frac{1-p}{p} \right)^k.
Osservazione. Se S è finito, allora esiste sempre almeno una misura invariante.
Infatti, se P è la matrice di transizione, essa è stocastica (la somma di ogni riga è 1), dunque:
P \begin{pmatrix} 1 \\ \vdots \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ \vdots \\ 1 \end{pmatrix}Questo implica che 1 è un autovalore di P, ovvero che la matrice (I - P) è singolare. Di conseguenza esiste un vettore riga non nullo \mu tale che \mu(I - P) = 0, ovvero \mu = \mu P.
Ricorrenza positiva e nulla
§ Definizione. Siano x, y \in S, il tempo medio \gamma_x^y, cioè il tempo trascorso in x tra due visite consecutive in y, è definito come:
\gamma_x^y = \mathbb{E} \left[ \sum_{n=0}^{T_y-1} \bbone_{\{X_n = x\}} \mid X_0 = y \right].§ Proposizione. Se la catena è irriducibile e ricorrente, allora:
\gamma_y^y = 1.(\gamma_x^y)_{x \in S}è una misura invariante.0 < \gamma_x^y < \inftyper ognix \in S.
Inoltre, se la catena è irriducibile ed esiste una misura invariante \rho tale che \rho_y = 1 per un certo y \in S, allora \rho_x = \gamma_x^y per ogni x \in S.
Osservazione. Notiamo che la somma dei tempi medi di permanenza è il tempo medio di ritorno:
\sum_{x \in S} \gamma_x^y = \sum_{x \in S} \mathbb{E} \left[ \sum_{n=0}^{T_y-1} \bbone_{\{X_n = x\}} \mid X_0 = y \right] = \mathbb{E} \left[ \sum_{n=0}^{T_y-1} \sum_{x \in S} \bbone_{\{X_n = x\}} \mid X_0 = y \right] = \mathbb{E} [T_y \mid X_0 = y].§ Definizione. Uno stato ricorrente y \in S si dice:
- ricorrente nullo se
\mathbb{E}[T_y \mid X_0 = y] = \infty. - ricorrente positivo se
\mathbb{E}[T_y \mid X_0 = y] < \infty.
§ Teorema. Se la catena è irriducibile, le seguenti affermazioni sono equivalenti:
- Ogni stato è ricorrente positivo.
- Esiste uno stato ricorrente positivo.
- Esiste una legge invariante.
Osservazione.
- Nella passeggiata aleatoria simmetrica su
\mathbb{Z}, gli stati sono ricorrenti ma la misura invariante\mu_k = 1non è sommabile, dunque gli stati sono ricorrenti nulli. - Se
Sè finito e la catena è irriducibile, allora tutti gli stati sono ricorrenti positivi.
Periodicità
§ Definizione. Il periodo di uno stato x \in S è definito come il massimo comun divisore dei tempi di ritorno possibili:
d(x) = \gcd \{n \ge 1 : p_{x,x}(n) > 0\}.Se d(x) = 1, lo stato si dice aperiodico.